ООО "МИГРАС" - молодая российская компания, миссией которой является разработка, внедрение и сопровождение современных IT-решений для компаний нефтегазового сектора, а также оказание информационно-консультационных услуг в данной области.
Разрабатываемые ООО «МИГРАС» программные продукты носят высокотехнологичный характер, представляя собой инновационные цифровые решения для сектора разведки и добычи, которые позволяют:
-
Сократить сроки и стоимость геологоразведочных работ
-
Повысить качество геологоразведочных работ
-
Снизить стоимость программного обеспечения
-
Перейти на российские программные продукты
-
Ответить на актуальные вызовы, стоящие перед недропользователями и сервисными компаниями
Гибкая система настройки цифровых решений, а также их совместимость с другими программными продуктами предопределяют возможность и простоту их использования на протяжении всего цикла поисков и разработки месторождений.
Наши партнеры

Команда ООО «МИГРАС» включает в себя высоко квалифицированных специалистов как в областях программирования, так и в области геологического изучения и разработки недр. Такое сочетание обеспечивает не только возможность создания цифровых решений, но и глубокое понимание решаемых геологических задач.
Разработка и сопровождение IT-решений для компаний нефтегазового сектора
Мы развиваемся при поддержке Фонда содействия инновациям fasie.ru
117105, г. Москва,
вн. тер. г. Муниципальный Округ
Донской, Варшавское шоссе, д. 33
ИНН - 9726000550
2024 © ООО "Миграс". Все права защищены
Политика конфиденциальности
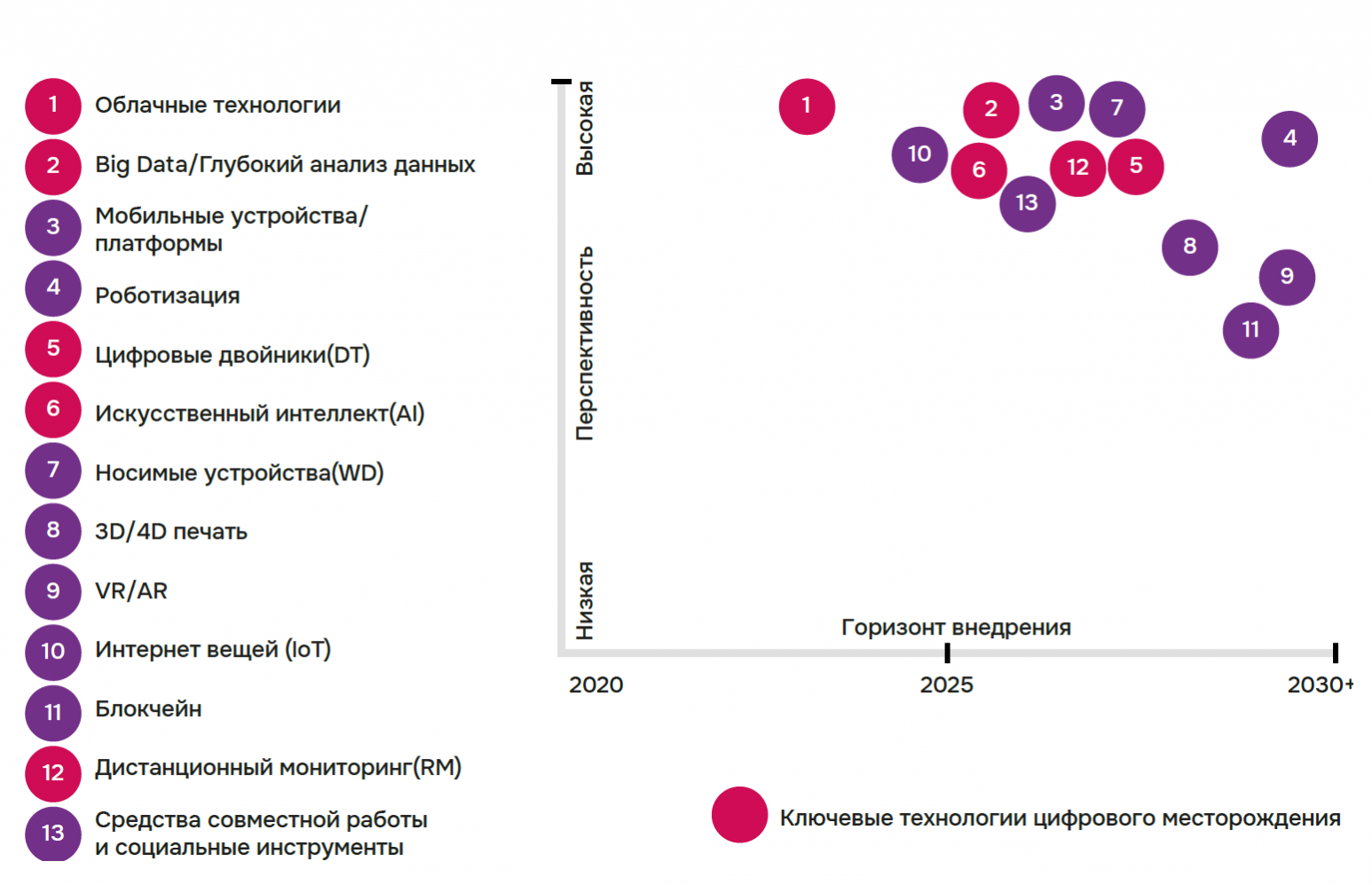
В научных кругах активно обсуждают цифровые инновационные решения в нефтегазовой отрасли, и эта тема активно поддерживается государством.
«Практически все нефтегазовые компании опираются на проект «Цифровая энергетика» в рамках государственной программы «Цифровая экономика».» (1)
«Применение IT-решений позволит повысить коэффициент извлекаемых запасов на 2–7% и при этом сократить операционные затраты на 25%.» (2)
(1) Галушко М., Дедеева С., Иневатова О. Цифровые инновационные решения, как основной инструмент повышения конкурентного преимущества предприятий нефтегазовой отрасли / Экономические науки № 1 (218)
(2) Клубков С., Мосоян М. Цифровая добыча нефти: тюнинг для отрасли / VYGON Consulting. 2020.
Отзывы
Наши заказчики говорят о Нас
«Использование в работе продукта MIGRaaS_PSTM позволило выполнить ряд миграционных преобразований на этапе обработки сейсморазведочных данных без установки дорогостоящего оборудования и его обслужвания. Подобная модель использования сервиса является удобной и практичной»
Геофизик, ведущий специалист сектора обработки
сейсморазведочных данных ЗАО «МиМГО»
Мы являемся участниками Московского инновационного кластера и состоим в реестре высокотехнологичных компаний г. Москвы (про нас)
Мы являемся финалистами программы ГАЗПРОМ НЕФТЬ INDUSTRIX (подробнее)
Наши достижения
«При оказании услуг в области предоставления IT-решений и их сопровождения сотрудники ООО «МИГРАС» показали себя как надежные и высоко квалифицированные специалисты не только в направлении работы с углеводородами, но и в области работы с твердыми полезными ископаемыми.
Мы намерены продолжать работу с данной организацией в этих двух направлениях»
Генеральный директор АО «УК Восток»
«Разработанное ООО «МИГРАС» программное решение* позволило на более качественном уровне выполнять работы по обработке сейсмических данных»
Генеральный директор ООО «ЦЭиРН»
* - по условиям лицензионного соглашения программное решение не может быть опубликовано
Мы являемся аккредитованной IT компанией
Наш проект интеллектуального интерпретационного сопровождения обработки сейсморазведочных данных SeisXpert принял участие в технологическом акселераторе INDUSTRIX 2025.
Он был отобран из более чем 400 конкурсных заявок, и вошел в двадцатку финалистов! По результатам конкурсного отбора так же вошел в тройку проектов, отмеченных специалистами Сбера, и на текущий момент готовится к ОПИ в периметре ПАО ГАЗПРОМ НЕФТЬ (диплом финалиста и тизер-видео)



